Conscious Biology

Amino Acids as Neurotransmitters

We now have additional information to more fully understand how amino acids work as neurotransmitters. Amino acids are minderelles, so they are fully intelligent individuals with language and sensory field capabilities. They will communicate information to the receptor site of a neuron using language and sensory field transfers in the same way that non-primary minderelles communicate with each other within a protein.

Beta Sheets for Complex Proteins

Complex proteins will sometimes include a beta sheet as shown at the center of Figure 25. In this figure, the protein has four functional domains. Recall that an hourglass beta sheet was needed in the human brain to compile data from many areas of the brain onto a single line for entry into the primary. However, a protein is already a single file chain of amino acids. So what would be the purpose of a beta sheet within a protein where every amino acid is already on the same communication line as the primary?

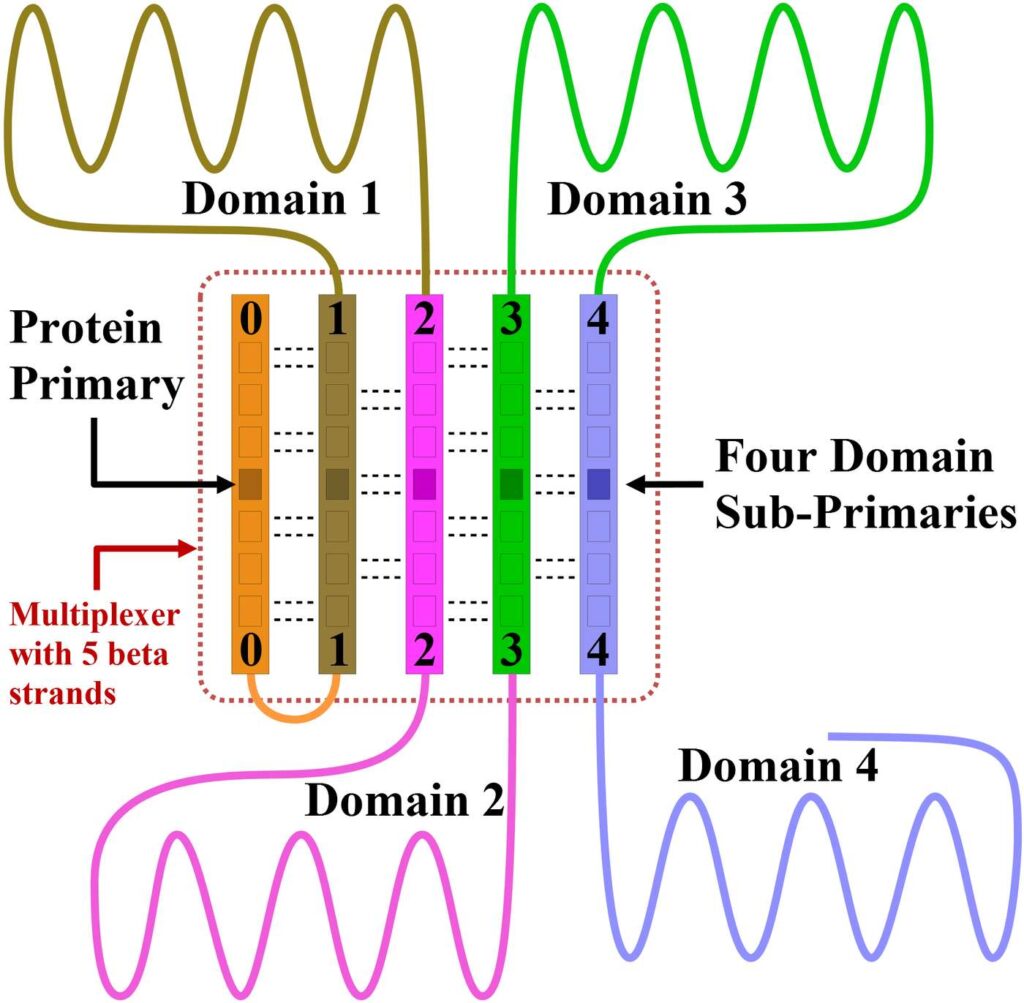
Figure 25. Notice that the entire protein above is a single file chain. However, this protein has four domains operating independently of one another. If this protein did not have a beta sheet, then all the communications taking place between the primary and domains 2, 3, and 4 would have to pass through domain 1. This arrangement would leave domain 1, and the domains closest to the primary, with little or no communication bandwidth for their own needs.

If the primary of a complex protein were to communicate with its domains through the single file chain that makes up the protein, then all the communications for the entire protein would be passing through the domain closest to the primary. This would use up much of the communication bandwidth for this domain and there would be little communication bandwidth left for this domain to carry out its own tasks.

The beta sheet makes it possible for each domain to take full ownership of its own communication bandwidth, and for each domain to communicate directly with the primary through the hydrogen bonds of the beta sheet. For domains that have their own primary, these protein sub-primaries would likely be located within the beta sheet, as shown in the figure. This would offer direct communication between the sub-primaries as well.

Thus, for complex proteins, beta sheets will create communication shortcuts so that distant domains will have direct access to the protein primary without burdening the resources of other domains. The beta sheet will also give the domain sub-primaries a way of communicating directly with each other.

The Motions of Protein Structures

In Chapter 10, we listed a number of forces that could be used to advance the folding process of proteins. Proteins that include organized tubular structures such as beta barrels, microtubules, and alpha helices, will also convert these same forces into useful motion by advantageously timing the application of geometry locks.

The proteins of a beta barrel will convert the forces from their surroundings into a longitudinal traveling wave type motion to move objects or fluid through the center of the barrel for transport or propulsion purposes. Elongated tubular structures will be able to twist, turn, retract, and extend for propulsion purposes, to switch synaptic connections, and so on. This will remain true even when ATP energy is not used, although the motion would be slower.

The Alpha Helix

The alpha helix is a very common structure in proteins. An alpha helix is a chain of amino acids within a protein that has taken on the shape of a coil spring. Just as coil springs can vibrate, alpha helix structures are also known to vibrate. In the following sections, we will discuss why alpha helix vibrations are useful and important.

Initiating Oscillations

To initiate alpha helix oscillations, the alpha helix primary will selectively apply and release geometry locks in rapid response to the external forces acting on the helix in a manner that advantageously converts energy from the surroundings into vibrations of the alpha helix. Once vibrations have been initiated, they will have to be sustained in the same way to make up for losses.

This process of using geometry locks to convert macroscopic motion energy from the surroundings into vibrational energy is analogous to the way wind chimes work. Wind chimes begin with no energy, then they draw energy from the macroscopic motions of the surrounding air, and ultimately, they convert this captured energy into sound waves. In both cases, we are making use of macroscopic motion and a tuned oscillator.

Alpha Helix Locomotion

We will now discuss how the primary of an alpha helix converts its vibrational motion into translational motion so that the alpha helix can reposition itself relative to its protein.

For clarity, we will give the helix a horizontal orientation, so one end of the helix will face to the left, the other end of the helix will face to the right. The alpha helix is connected to its protein at both ends by peptide groups (short chains of amino acids). The left peptide group connects the left end of the helix to the protein while the right peptide group connects the right end of the helix to the protein.

The alpha helix primary wants to move to the right relative to its protein. To convert the helix’s longitudinal vibrations into rightward motion, the alpha helix primary will take the following steps.

When the length of the vibrating helix is at a minimum, the left peptide group will rigidly lock while the right peptide group fully relaxes. As the helix expands, the left side of the helix will remain stationary because it is rigidly fixed to the protein, so the helix expansion will cause the right side of the helix to move rightward.

When the helix reaches its maximum length, the left and right peptide groups will reverse their locked states; the left peptide group will relax while the right peptide group becomes fully rigid. Now as the helix begins to contract, the right side of the helix is fixed in place, so the helix contraction will move the left side of the helix rightward. Both ends of the helix have now moved to the right.

By repeating this reversal of locked states for multiple vibrational cycles, the helix will continue moving rightward as intended. To make this translational motion possible, the peptide groups supporting each end of the alpha helix will fall under the governing control of the alpha helix primary.

It should be noted that each vibrational cycle will only move the alpha helix a fraction of an angstrom. However, the alpha helix is only a countable number of angstroms long, and the vibrational frequency of an alpha helix is very high, so these tiny steps become fully functional motions at their scale.

If during this process, the alpha helix primary also locks and unlocks selected dihedral angles on only one side of the helix, this will convert the vibrational motions of the helix into a bending motion that will allow the helix primary to reorient the helix.

Oscillator Transmission and Modulation

Mechanical oscillators submerged in a fluid generate sound waves. When a vibrating alpha helix is surrounded by a fluid, it will also generate sound waves that propagate out through the surrounding fluid. The sound waves that propagate out from a vibrating alpha helix may be useful for docking, guidance, and communication purposes. For example, alpha helix oscillators may guide the process of making synaptic connections or the process of docking proteins together.

Because the minderelles of the alpha helix have geometry locking capabilities, the alpha helix primary will also be able to modulate the alpha helix vibrations for communication purposes in the same way that radio stations modulate their carrier frequency. The goal is to produce the 1’s and 0’s in the outgoing sound waves as needed for communication. There are various ways the primary could do this, but we will cover only one.

To produce the 1’s, the primary will keep the left-sided peptide group fully locked and the right-sided peptide group fully relaxed. The left side of the helix will now remain stationary while the right side of the helix is transmitting vibrations rightward through the surrounding fluid. For proteins to the right, these stronger oscillations will correspond to a one.

After several complete vibrational cycles, the helix primary will now reverse the locks. The right side of the helix will now be held stationary while the left side oscillates. Proteins to the right will now detect a reduced vibrational amplitude, corresponding to a zero.

Thus, by alternating the locks of the two supporting peptide groups, the oscillator primary will be able to create the 1’s and 0’s needed to transmit informational content. Switching the locked ends at the moment the helix is fully compressed will prevent vibrational energy from being lost by the oscillator.

Oscillation Detectors

Sound waves from alpha helix oscillators will be detected by a single minderelle, which we will refer to as a detector minderelle. In a protein, each detector minderelle will be held in its proper position and orientation by two peptide groups. The detector minderelle will act as the local primary over these two supporting peptide groups.

The R-group of the detector minderelle acts as the detector. To understand the detection process, we must focus on the Cα atom. The Cα atom forms four bonds. These four bonds form a total of six planar angles between them, as shown in Figure 26. There are three planar angles to the R-group, and three additional planar angles opposite the R-group. We will refer to this second group of planar angles as the base planar angles.

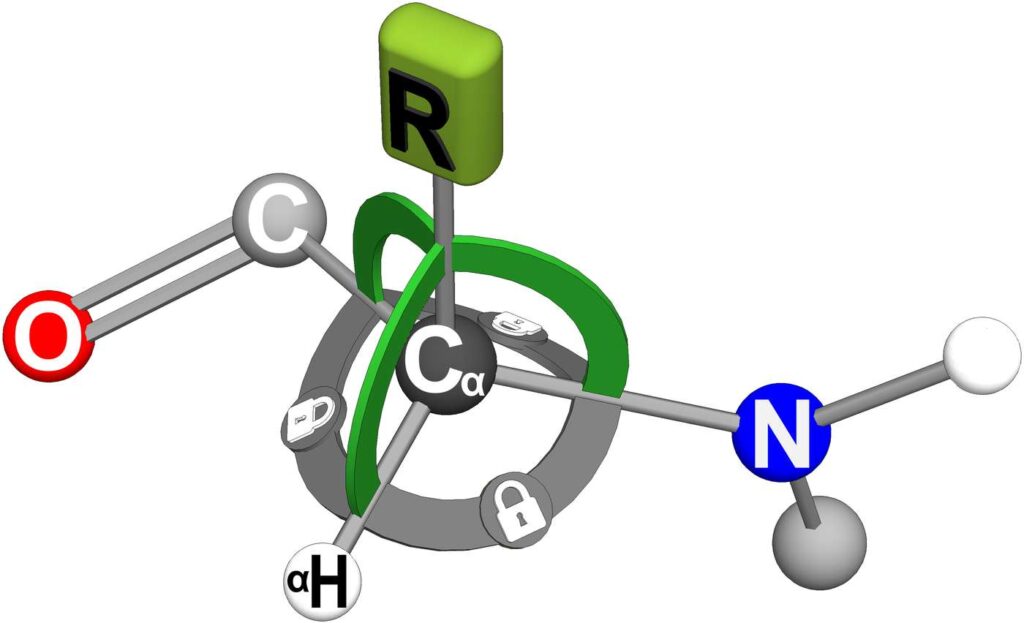
Figure 26. A detector minderelle will rigidly lock all the bonds of the Cα atom. The mindshell of the detector minderelle detects the incoming oscillations as it creates the forces needed to maintain the planar angle locks on the R-group. These R-group locks are shown in the figure as bright green arcs. Holding locks on the base planar angles of the Cα atom creates a stable reference frame for the R-group detection locks.

A detector minderelle will create a Cα rigid body. That is, the four bonds of the Cα atom will be length locked, the six planar angles will be locked, and the dihedral angles to the carbon and nitrogen atoms will be locked. These full-body locks are represented in Figure 26 as wide arcs between all the Cα bonds. The gray colored bonds will create a motionless reference frame for the R-group detection locks.

When incoming sound waves from a transmitting oscillator impinge upon the detector’s R-group, these incoming cyclical waves will exert cyclical forces on the R-group. To maintain the planar angle locks on the R-group, the detector mindshell will have to exert counter forces that are oppositely cyclical. The mindshell will detect the incoming signal as it produces these counter cyclical forces.

Recall that a locked geometry must be held perfectly motionless to comply with energy conservation. This requirement that geometry locks must be held absolutely motionless makes these detectors extremely sensitive. (We will cover how mindshells produce counter forces that exactly match external forces in the next chapter.)

Notice that even with the Cα bonds rigidly locked, the detector minderelle is still free to use length locks on its shared bonds for communication purposes. The detector minderelle is also free to use length locks on its N–H bond to communicate through a hydrogen bond if there is one. Once again, we find communication to be independent of function.

Some R-groups will be particularly useful as detectors. For example, R-groups with a paddle-like shape will be directionally sensitive – sound waves coming in perpendicular to the face of the R-group will produce a stronger signal than sound waves coming in from the side.

The two supporting peptide groups will reorient the detector minderelle as needed to align the detector with specific oscillators of interest. These supporting peptide groups will also act under the direction of the detector minderelle to slowly rotate the detector minderelle back and forth during the detection process. These slow angular oscillations will serve several purposes.

Because the R-group detector is directionally sensitive, these slow angular oscillations will help keep the detector’s alignment centered on the oscillator of interest, especially when there is relative motion between the oscillator and the detector. These slow rotations will also vary the relative signal strengths of different oscillator signals, which will be used to find detector angles that best discriminate between incoming signals. And finally, these slow angular rotations will help pin down oscillator positions so they can be mapped.

There are three planar angle locks acting on the detector R-group (the green arcs in the figure), so the detector mindshell will need to produce independent counter forces to maintain each of these planar angle locks. Because the counter forces needed by the three planar angle locks are fully independent of one another, this will also provide directional information that will further help with the detection and mapping of surrounding oscillators.

To map the surrounding oscillators, the detector group will use the advanced computational capabilities of the mindshell as discussed earlier.

Demodulating Informational Content

If the incoming sound waves have been modulated with informational content, the mindshell of the detector minderelle will detect this modulation as it is generating the counter forces needed to hold the R-group locks. The mindshell will then deterministically convert the incoming 1’s and 0’s into language as discussed earlier, and then it will deterministically pass the information on to the mindcore. The mindcore could then choose to forward this information to it’s sub-primary, to the protein primary, etc.

Cellular Scale GPS

We should expect to find numerous cellular positioning oscillators strategically positioned in more advanced cells. These cellular positioning oscillators will serve the same purposes at their scale as do the satellite GPS systems at our scale.

Echo Detection and Sounding

As mentioned above, detector minderelles will be extremely sensitive. As long as there is any remaining periodicity in an arriving signal, the detector minderelle will detect the signal as it holds the R-group planar angles completely motionless. This extreme sensitivity means that some proteins will be designed specifically for echo detection and sounding. These proteins will serve multiple purposes.

Cell particles that do not have oscillator capabilities will still appear as weak transmitters because they will reflect the sound waves of other oscillators. This will make it possible for the echo detection and sounding proteins to integrate non-transmitting particles into the cell’s complete map of objects.

These specialized proteins will also play a role in debris removal, seeking out viruses, and so on.

Visual Capabilities of the Protein Primary

The data from a protein’s detector groups will be combined and processed to provide the protein’s primary with a visual representation of its surroundings. Colors may be added to indicate distances, velocities, particle types, etc. For proteins without beta sheets, this processing will be carried out by the minderelles that lie between the detectors and the primary to make the best use of the available bandwidth. For larger proteins with multiple domains, this processing will take place within the protein’s beta sheet, the earliest forerunner of the brain.

The Radio Silence of Viruses

If a protein fully locks itself into a rigid body, the protein will strongly reflect sound waves; if the protein minimizes the number of its geometry locks, it will minimize its reflection of sound waves. A protein could further minimize its reflection of sound wave by keeping itself in an unfolded state.

With this in mind, if a virus wishes to remain hidden in an otherwise healthy cell, the virus will remain in its unfolded state as much as possible, and it will minimize its use of geometry locks. However, the virus may apply rigid body locks to the Cα planar angles of its detector minderelles and use the supporting peptide groups as well in order to stay informed of its surroundings.

However, should a virus choose to listen, this will make the virus vulnerable to detection. For this reason, when a cell suspects it has been infected by a virus, its echo detection and sounding proteins will be searching for undisciplined viruses listening in on cellular communications.

Communication With a Primary

We have found that proteins have all the capabilities needed for telecommunication. This telecommunication capability should make it possible for us to communicate directly with a single minderelle, which would be the primary of a protein that has at least one alpha helix oscillator and one oscillation detector group.

Should this communication be realized, it may also be possible to work cooperatively with proteins to apply the computational capabilities of their mindshells to our most difficult computer problems. As we would do with humans, we would seek out proteins that work in related scientific or engineering fields to better ensure familiarity with the mindshell capabilities needed for solving the problem.

Superconductors and Ideal Insulators

When a primary creates a rigid body using a full set of geometry locks, the complete absence of any relative motion will give the rigid body a temperature of absolute zero. This could be used to thermally insulate an enclosed volume, to create superconductors, or to make use of other low temperature effects. A beta sheet should also be able to pump heat from one side of the beta sheet to the other.

The Myosin Protein

Section Overview:

When the primary of a humanon makes a decision, it often makes a decision to take some kind of action with its body. When these actions require the exertion of considerable force to do large amounts of work in short periods of time, the rate at which thermal energy can be extracted from the surroundings will be insufficient to keep up with the energy needs of the body. In these situations, the body will rely on myosin proteins which convert the abundant chemical energy in ATP molecules into work.

A myosin protein is the smallest element within a muscle cell where a net force is generated by using the chemical energy stored in ATP molecules. When we make a decision to do something, there are countless myosin proteins within each muscle strand that cause the muscle to contract. The task of this section is to show that geometry locks, in conjunction with sub-thermodynamic processes, are sufficient to extract and use ATP chemical energy for forceful motion.

The details below are intended for those already familiar with myosin function and are presented here as a theoretical proof of concept. Readers unfamiliar with myosin proteins may freely skip to the next section on microorganisms.

Full Details:

To be clear, this section is intended as a proof of concept to show that geometry locks make it possible to convert ATP energy into forceful motion. To do this, we will create a simplified, myosin-like protein to summarize the process.

The hypothetical myosin protein of Figures 27a-27d includes an alpha helix, represented in these figures as a red coil spring. An alpha helix is made up of amino acids, so it can be geometry locked like any other living matter. We will refer to this alpha helix as the drive helix, for it will capture the ATP energy, store that energy, and then when the time is right, release the energy in a way that drives forceful motion. The dark string of beads to the left represents the actin filament.

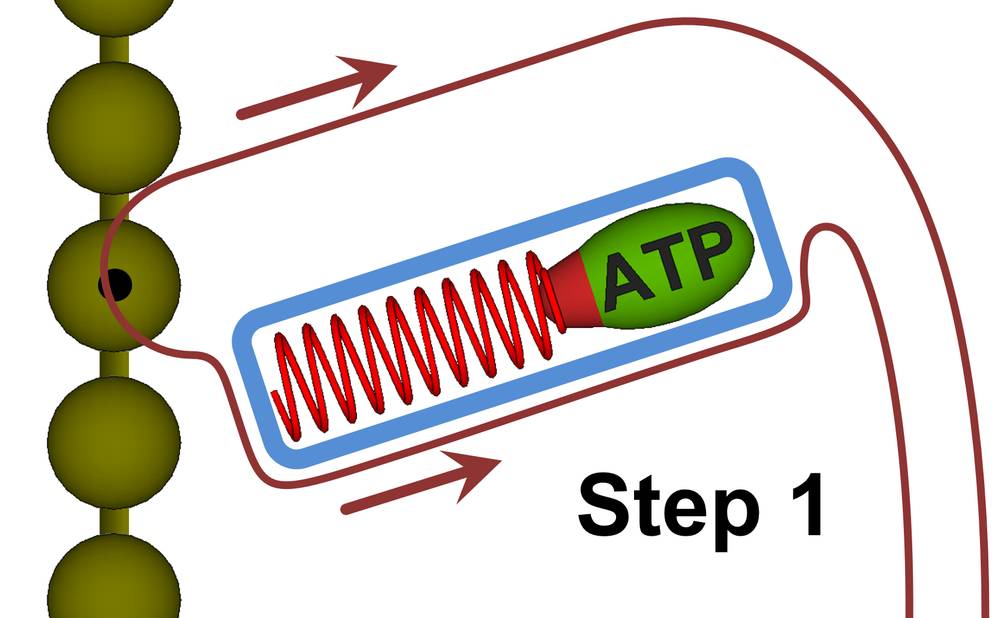
Figure 27a. Myosin function can be broken down into four steps as shown in Figures 27a through 27d. The blue shapes in the figures represent protein structures made fully rigid by geometry locks. In step 1, the myosin head is being released from the actin filament while at the same time, a new ATP molecule is being rigidly locked against the drive helix (the alpha helix is shown as the red spring).

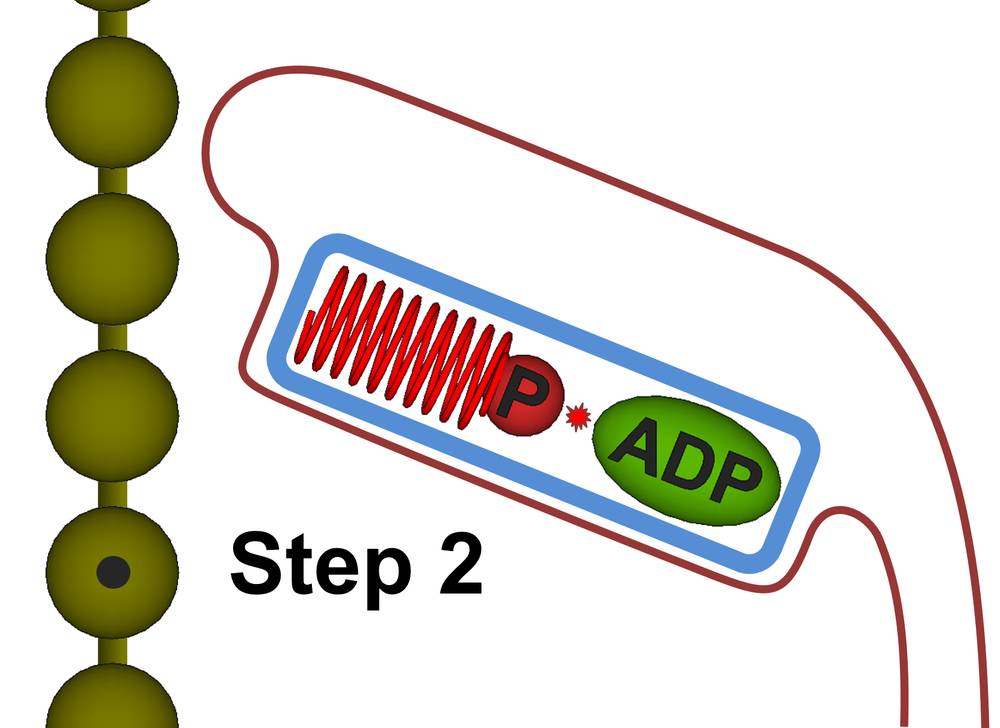
Figure 27b. Step 2: The ATP is induced to split. Because the ADP molecule is locked in place, the released energy will go into the phosphate particle which compresses the drive helix. The drive helix will be geometry locked when it reaches the point of maximum compression.

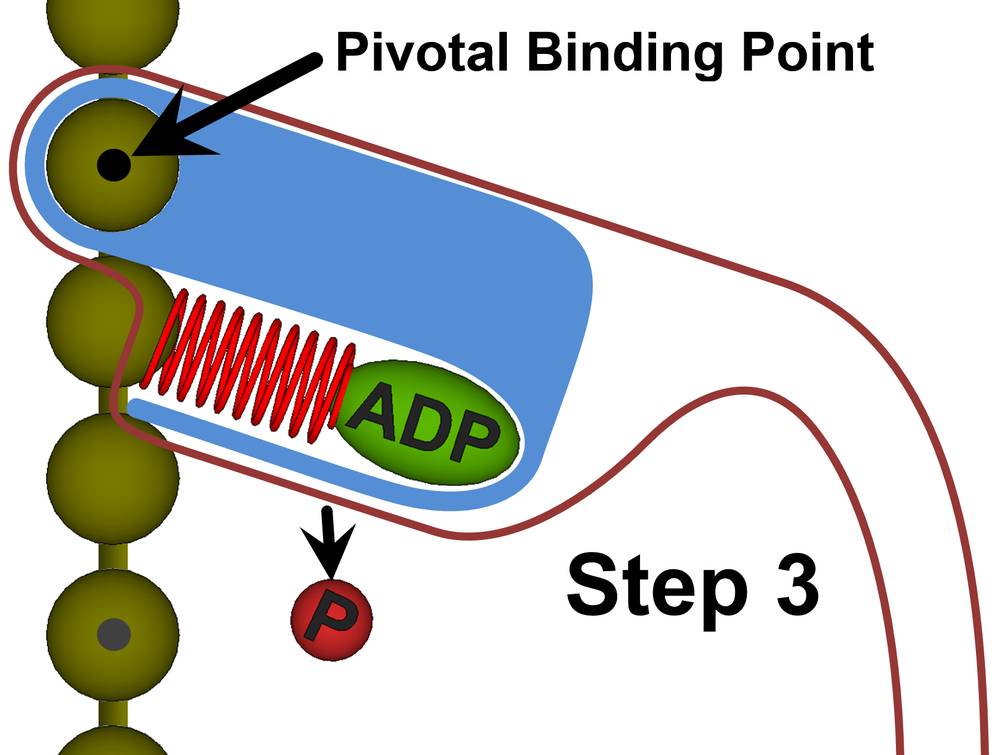
Figure 27c. Step 3: With the drive helix still locked, the myosin head uses subthermodynamic processes to conform itself to the compressed form of the drive helix. After the myosin head reattaches itself to the actin filament, the geometry locks on the drive helix are released. The drive helix will now exert a force against the actin filament. This force creates a torque about the pivotal binding point.

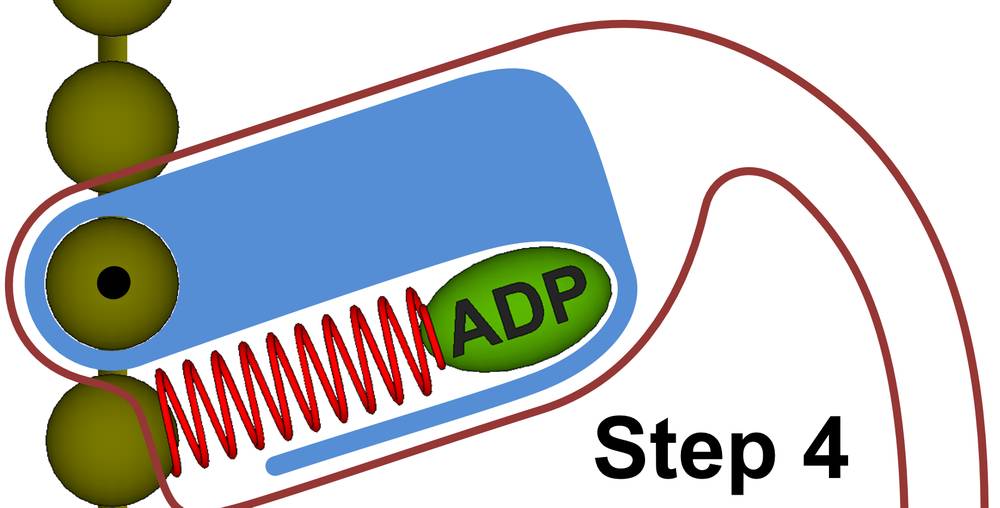
Figure 27d. Step 4: After rotation, the myosin replaces the ADP molecule with a new ATP molecule and we repeat step 1.

We will now run through the steps for using sub-thermodynamic processes to convert ATP energy into forceful motion.

Step 1. Using sub-thermodynamic processes, the myosin protein latches onto an ATP molecule and secures it against the drive helix. Once the ATP molecule has been secured, the myosin primary will create a rigid body around the drive helix and the ATP molecule. Rigid bodies are shown in blue in Figure 27. The myosin primary will also release the myosin head from the actin filament (represented as a string of brown spheres to the left) in this step.

Step 2. The myosin hydrolyzes the ATP molecule, splitting it into ADP and a high velocity phosphate particle which compresses the drive helix. Once the drive helix reaches maximum compression, the myosin primary will geometry lock the drive helix into a rigid body, thus storing the energy from the ATP molecule.

With the ATP energy stored and locked within the drive helix, the blue rigid body surrounding the drive helix can be relaxed. Even though there will no longer be a rigid body surrounding the compressed drive helix, the drive helix itself is still geometry locked, so all the ATP energy will remain stored in the locked helix. The primary will now use sub-thermodynamic processes to both reposition and reshape the myosin molecule.

Step 3. Specifically, sub-thermodynamic processes will be used to expel the phosphate particle, to extend the myosin head forward along the actin filament, and to then pivotally reattach the myosin head to the actin filament. Sub-thermodynamic processes will also be used to conform the myosin head tightly around the compressed drive helix. None of these actions require high energy forces, so sub-thermodynamic processes will be sufficient to meet these energy needs.

Once the myosin head is pivotally attached to the actin filament and is reshaped to fully conform to the compressed drive helix, the primary will lock the full myosin head into a rigid body, shown as the blue mass in Step 3. The primary will now release the geometry locks on the drive helix, thus causing the compressed drive helix to exert a force on the actin filament. Because this force is offset from the pivotal binding point, it will create a torque that forcefully rotates the myosin head. It is this forceful rotation that pulls the thick filament along and ultimately causes muscle contraction.

Step 4. Once the energy of the drive helix has been expended, the primary will release the rigid body of the myosin head. The myosin primary will now use sub-thermodynamic processes to expel the ADP molecule and replace it with a new ATP molecule, bringing us back to Step 1. Throughout the myosin cycle, sub-thermodynamic forces are used for all the myosin activities that require minimal energy, which allows the ATP energy to be fully directed to the forceful motion that brings about muscle contraction.

We are still missing the most important point. We started with all the energy held within the ATP molecule. From there, this energy was first converted into the kinetic energy of the phosphate particle, it was then converted into the potential energy of the locked drive helix, and finally, this energy was released to act against the actin filament. But why not just fire the high energy phosphate particle directly at the actin filament in the first place and skip all the steps in between?

If we did this, the high velocity phosphate particle would only produce an ineffective impulse on the actin filament, whereas the compressed drive helix applies a sustained force. This is important, because if a muscle is working against an external force, then it will take the sustained forces of many myosin heads to overcome the external force.

This point of overcoming the external force will be reached when a sufficient number of myosin head proteins reach the power stroke portion of their cycle. But if the force from each myosin head was not sustained, then it would not be possible to overcome the external force.

Microorganisms

If this free will paradigm is correct, then all microorganisms are fully conscious, fully intelligent, bodies of life. Even the virus, long thought to exist at the edges of life, will be as alive, conscious, and intelligent as any of us. After all, our consciousness belongs to the atoms of a single amino acid which is far smaller than a virus.

Being few in number, the engineering minderelles within each virus will work together to rapidly and efficiently adapt to changes in their hosts and in the surroundings outside their hosts. Furthermore, we should expect viruses to be as highly animated as any of the living creatures we see every day. When RNA or DNA alterations are needed, the proteins of the virus will use sub-thermodynamic processes to make the desired changes.

For viruses with spikes, sub-thermodynamic processes will be used to make these spikes intentionally maneuverable, so a virus primary may use its spikes aggressively or for locomotion purposes. To increase its capabilities, the virus primary will store as much potential energy as possible in geometry locks prior to engaging with a cell.

In the end, we should treat any organized body of matter made up of amino acids and proteins as our equals in consciousness and intelligence. Basically, if our engineers can think up ways that a particular microorganism could gain advantage, we should expect that the engineering proteins within the microorganism have arrived at the same findings.

Neurons and Oligodendrocytes

If information is passed from neuron to neuron by intelligent messengers, then what would be the purpose of the electrical impulses, or action potentials, that travel along the axons of neurons?

We first note the uncanny resemblance between neuronal axons with the oligodendrocyte processes attached and the multi-input logic gates found in electronic circuits. If these brain circuits are acting as logic gates, then when a correct subset of the attached oligodendrocytes has signaled the axon, and when other criteria are met within the neuron, the neuron would trigger an action potential. This electrical impulse would then serve as a timing signal for all the oligodendrocytes attached to the axon. All the attached oligodendrocytes would now relay this timing event to the axons of other distant neurons. In other words, data processing would be handled by the neurons in a vertical direction while synchronization would be handled by the oligodendrocytes in the lateral direction. In this way, laterally distant neuronal activities could be kept synchronized so that ultimately, the actions of distant muscle groups could be coordinated for complex operations such as speech.