Chapter 14
The Physics of Consciousness
Note to Lay Readers
This chapter will cover the physics details of this free will paradigm, details that will be important to physicists and other scientists. Lay readers should feel free to skim through this chapter or skip to the next.
Holding Geometry Locks During Collisions
We found that conscious minds can change physical events by using geometry locks. However, minderelles are jostling non-stop with their surroundings. For the geometry locking solution to be useful in the real world, minderelles will have to be able to impose and hold geometry locks even as these geometry locked atoms are undergoing collisions with surrounding atoms. In the next few sections, we will cover important and practical details about geometry locks.
In Figure 28, a mind is attempting to hold a length lock on the A1–A2 bond, but particle P is colliding with atom A1. The collision force is represented by the red repulsion lines between P and A1, where the collision force is Fcollision.
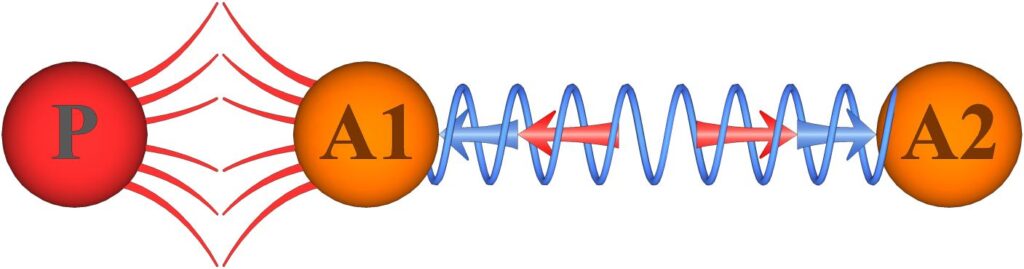
Figure 28. Particle P is coming in from the left and is colliding with atom A1. A mind has imposed a length lock on this bond, so it is applying the blue mind forces to counter the bond force. The mind had to add the additional red mind forces to counter the collision force in order to maintain its length lock.
Prior to the collision shown in Figure 28, the blue mind forces were the only forces needed to hold the length lock. However, the collision force acting on A1 will push A1 closer to A2 and break the length lock unless the mind acts to counter the force of the collision. In the figure above, the mind has added the additional red force pair to hold its lock and keep the distance between A1 and A2 constant during the collision. In keeping with the zero-sum rule, this additional force pair must always be equal and opposite.
For the example shown in Figure 28, the instantaneous magnitude of the red mind forces needs to be,

where M1 and M2 are the masses of atoms A1 and A2, and Fcollision is the collision force that particle P is exerting on atom A1. This equal and opposite counterforce pair (the red arrows in Figure 28) will cause both A1 and A2 to accelerate to the right at exactly the same rate, thus keeping A1 and A2 exactly the same distance apart and maintaining the mind’s length lock on the bond. This shows that it is possible for length locks to be held even during collisions.
Although we were able to calculate the instantaneous magnitude needed for a counterforce pair during a collision, in the real world, having a mind generate these counterforce pairs on the fly would not be so straightforward. Collisions will take place with multiple outside bodies simultaneously, and the moment to moment progression of the collision forces acting on the locked atoms would seem to be unpredictable for the mind.
For a mind to hold a geometry lock during collisions, the mind would have to predict the exact strength of the counterforce pair that would be needed in the momentary future so that it could meet the continuously changing collision forces with exact and continuously correct counterforces. This requirement for instantaneous response times is seriously problematic in physics, so it will have to be addressed. We do not yet have all the information needed to solve this problem, so we will hold off on finding a solution until later in the chapter.
Mind Forces Doing Work
In Figure 28, notice that there is a net force acting on atom A2. The rightward blue mind force acting on A2 counters the blue bond force, but the rightward red force is not opposed and ends up creating a net force on A2. It is this net rightward force that is causing the A2 atom to accelerate to the right at the same rate as A1. However, this means we now have a mind force causing the acceleration of the A2 atom, so the mind force accelerating A2 is doing work.
The red mind force acting on A2 is adding energy to the universe, which does not seem consistent with our original goal. We started out looking to find a way for minds to exert real forces that do zero work while still changing physical outcomes, but we ended up with a geometry locking solution where we have mind forces doing work during collisions. Would this not mean that the geometry locking solution violates the conservation laws during collisions and fails?
It does not mean this. In physics, work can be positive or negative, so even though an individual mind force may be doing positive work, the sum of the work being done by all the mind forces can still be zero. In this case, the mind is doing positive work by accelerating A2, but the same mind is also doing negative work by acting on A1 in the opposite direction. Because the two atoms are accelerating in the same direction at the same rate, the work being done by the two red forces sum to zero. As long as the bond length does not change, the total work being done by the mind will be zero.
Therefore, the length lock makes it possible for a mind to exert real forces that change real outcomes without violating any of the conservation laws, and this holds true even during violent, complex collisions. The same logic can be generalized to show that planar angle locks and dihedral angle locks will also comply with all the conservation laws, even during complex collisions with surrounding atoms.
Energy Redistribution
Geometry locking mind forces will sometimes redistribute the energy within a system, but they will do zero net work in the process. The length lock shown in Figure 28 is redistributing the kinetic energy of the system without changing the total energy. In other cases, geometry locks will redistribute the potential energy within a system, or they will sometimes convert one form of energy into another. However, in all cases where geometry locks are applied, the total energy of the locked system will always remain constant as long as the locked geometry is held frozen.
Geometry Locks for Angles
In these next sections, we will cover the forces needed for locking both planar angles and dihedral angles. These two types of geometry locks will create rigid geometries that still allow some relative motion to take place between the atoms involved. For example, a planar angle lock will lock the planar angle formed by two bonds, but the planar angle lock will still allow the lengths of the two bonds to vary.
Planar Angle Locking Forces
Figure 29 shows two bonds forming the planar angle θ. In a planar angle geometry lock, mind forces will hold the planar angle formed by two bonds constant while still allowing the lengths of the two bonds to vary freely.
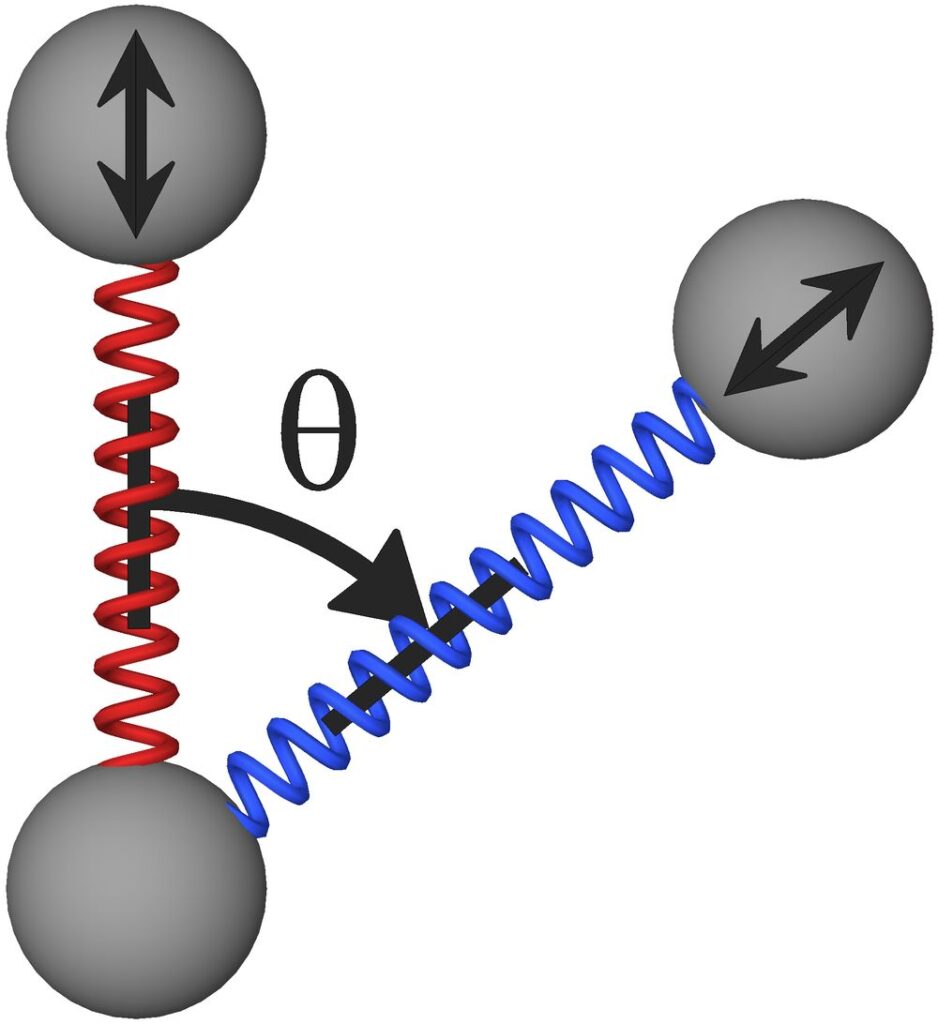
Figure 29. The red and blue bonds form planar angle θ. Notice that the angle θ can remain constant even while the lengths of the two bonds vary. Thus, the planar angle geometry lock will still allow some constrained relative motion to take place between the three atoms that make up the planar angle.
Failed Planar Angle Locking Forces
Figure 30 shows the mind force pair that would offer the easiest solution for locking a planar angle. This mind force pair is simply a pair of equal and opposite forces pushing the two outer atoms directly towards each other. However, this is not an acceptable locking solution.
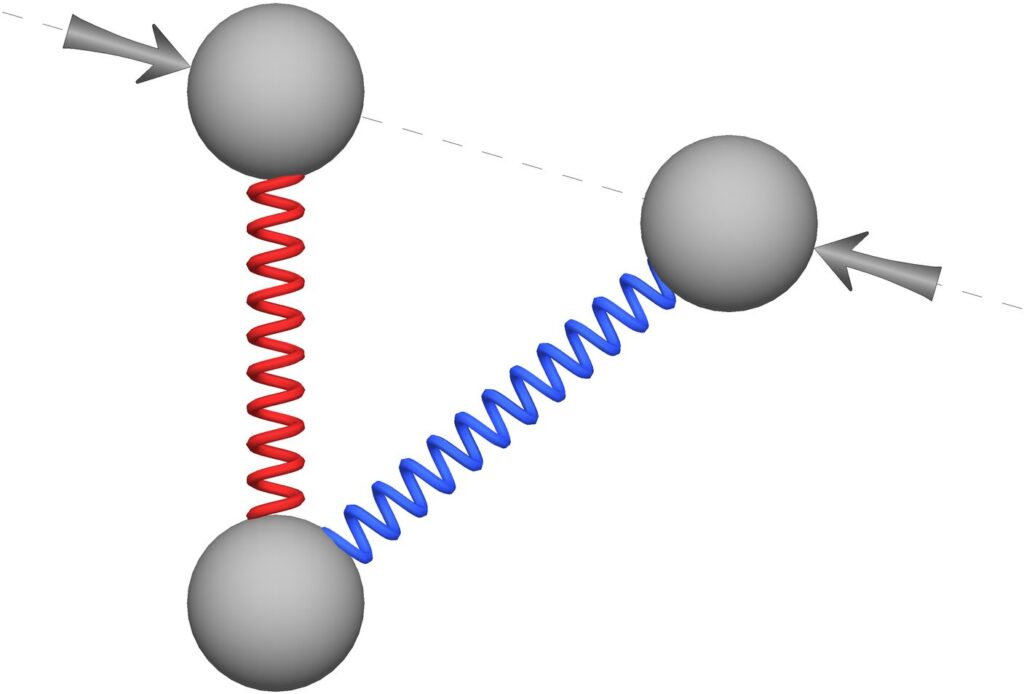
Figure 30. While the force pair shown in this figure would be capable of locking the angle shown, there are reasons the mind forces shown here cannot be allowed for planar angle locks.
Although the mind forces shown above are not acceptable, it is still instructive to review this apparent solution quickly to better understand mind forces in general. We will start by pointing out the good reasons for thinking the force pair shown in Figure 30 should work for locking a planar angle.
The pair of forces shown in Figure 30 are equal and opposite, so they are zero-sum as required by the zero-sum rule. Also, these two forces could push inward, or outward, to hold the angle wherever it is, so the forces shown could actually lock the angle. So why is there a problem?
First, this pair of mind forces is not acting across a molecular bond as required by the bond control rule. Minds govern across bonds, and there is no molecular bond between the two outer atoms being acted upon.
Second, the requirement that the forces and the torques of a mind sum to zero is a necessary condition for complying with the conservation laws, but it is not a sufficient condition. In other words, we can have equal and opposite mind forces where the sum of the forces and torques adds up to zero, but still ends up violating the conservation laws. That is the problem we have here.
While the mind forces shown in Figure 30 may be capable of locking the angle θ as shown, the bond lengths remain free to vary. If the bond lengths are changing while the angle is held constant, the distance between the two locked atoms would be varying and the mind forces would now be doing net work. Therefore, to lock an angle, we cannot have a force component parallel to the bonds that make up the angle.
The Torque Pair
Because the forces locking molecular angles cannot be allowed to work on the adjacent bond lengths, angle locking forces will have to be perpendicular to the bonds they govern. Figure 31 shows a mind force pair used to impose angle locks.
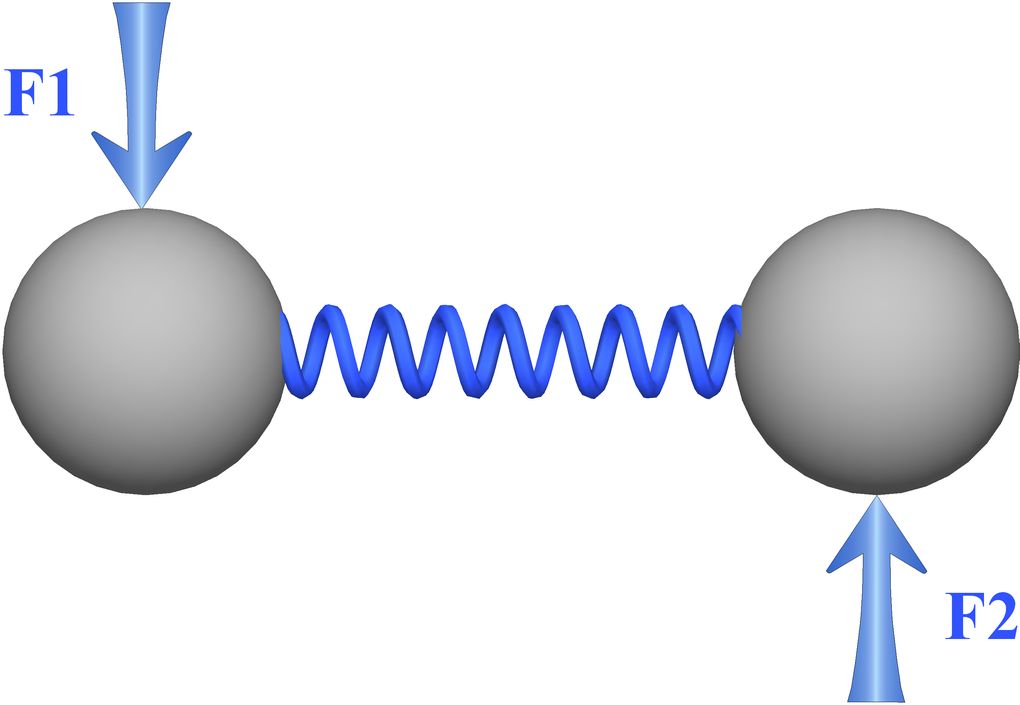
Figure 31. Mind force pairs used for locking angles will be perpendicular to the bonds they govern. Together, the forces F1 and F2 create a torque, which is needed to control an angle. An equal and opposite torque will be applied to the adjacent bond to lock the planar angle and zero out the total torque.
The forces shown in Figure 31 are acting across a molecular bond as required by the bond control rule, they are perpendicular to the bond, so they will not do work as the length of the bond changes, and they are equal and opposite, so they will not affect net momentum. We will refer to two forces working across a molecular bond to create a torque as a torque pair.
This pair of forces does, however, create a net torque that makes the bond and atoms want to rotate in a counterclockwise direction. To zero out this torque, as required by the zero-sum rule, minds will lock angles by using two equal and opposite torque pairs.
Torque Pairs Holding Planar Angles
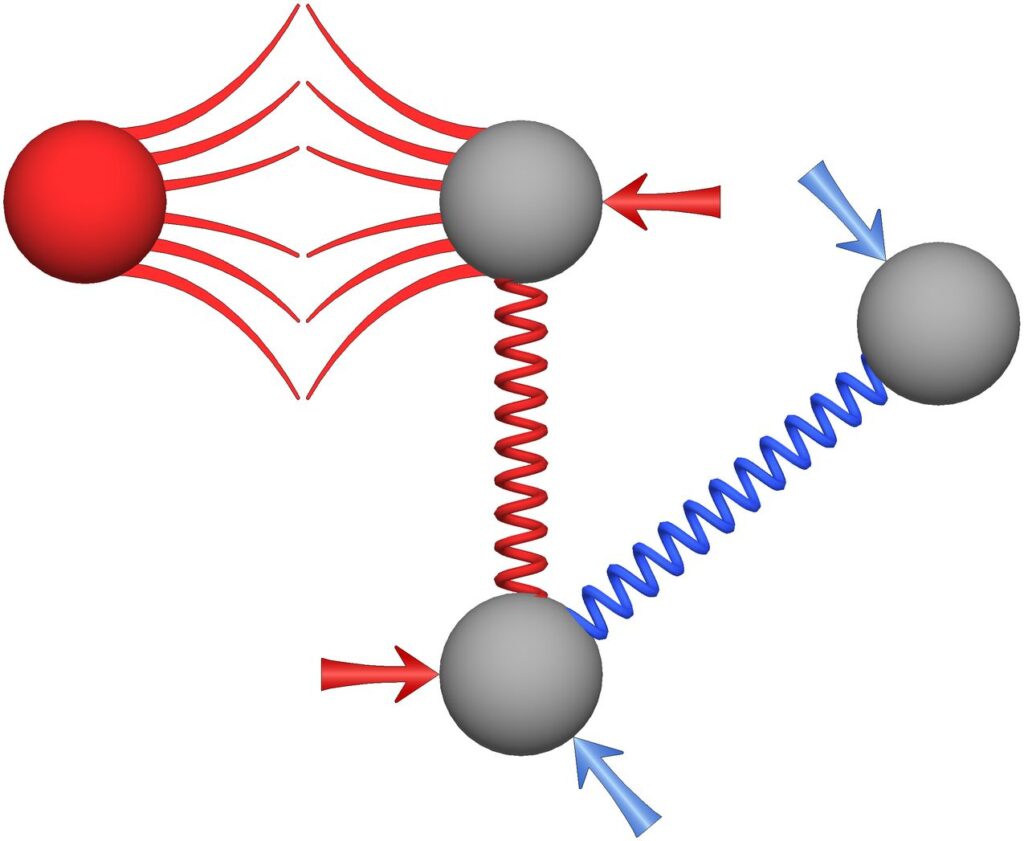
Figure 32. The red particle is coming in from the left such that the collision force is acting against a locked planar angle.
Figure 32 shows how two torque pairs are used to hold a planar angle lock during a collision. In Figure 32, the red torque pair is acting across the red bond while the blue torque pair is acting across the blue bond. The forces acting across the blue bond will be related to the forces acting across the red bond as follows,
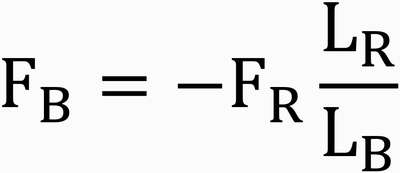
where LR and LB are the lengths of red and blue bonds, and FR and FB are the forces acting across the red and blue bonds. The two torque pairs are equal and opposite to one another, and the forces making up each torque pair are also equal and opposite, so both the total force and the total torque sum to zero in compliance with the zero-sum rule.
However, as we saw with the failed planar angle locking forces, compliance with the zero-sum rule makes compliance with the conservation laws possible, but not necessary (the zero-sum rule is a necessary condition, not a sufficient condition). So will planar angle locking forces be compliant with the conservation laws for the collision shown in Figure 32?
In particular, notice how the two forces acting on the lowest atom in Figure 32 each have a force component acting against the length of the opposite bond (the red force is acting against the blue bond and the blue force is acting against the red bond). If the two bond lengths are changing, then these two forces will now be doing work on these opposite bonds.
What matters in the end, though, is that energy be conserved – the total work being done by all the forces of the mind must not violate energy conservation. So again, when taken as a whole, are the planar angle locking forces of this example compliant with the conservation laws? And more generally, will planar angle locking forces be compliant with the conservation laws for any and all collisions?
The answer is yes, planar angle locking forces will always be compliant with the conservation laws. While physicists will be able to show this mathematically, lay readers can intuitively see why this is true by considering a hypothetical model of the planar angle lock built with idealized physical hardware. The hardware shown in Figure 33 was built to match the matter shown in Figure 32, but with idealized hardware at our own scale. Just as in Figure 32, the lengths of the “bonds” in our model are also free to vary and the angle between the bonds is also locked.
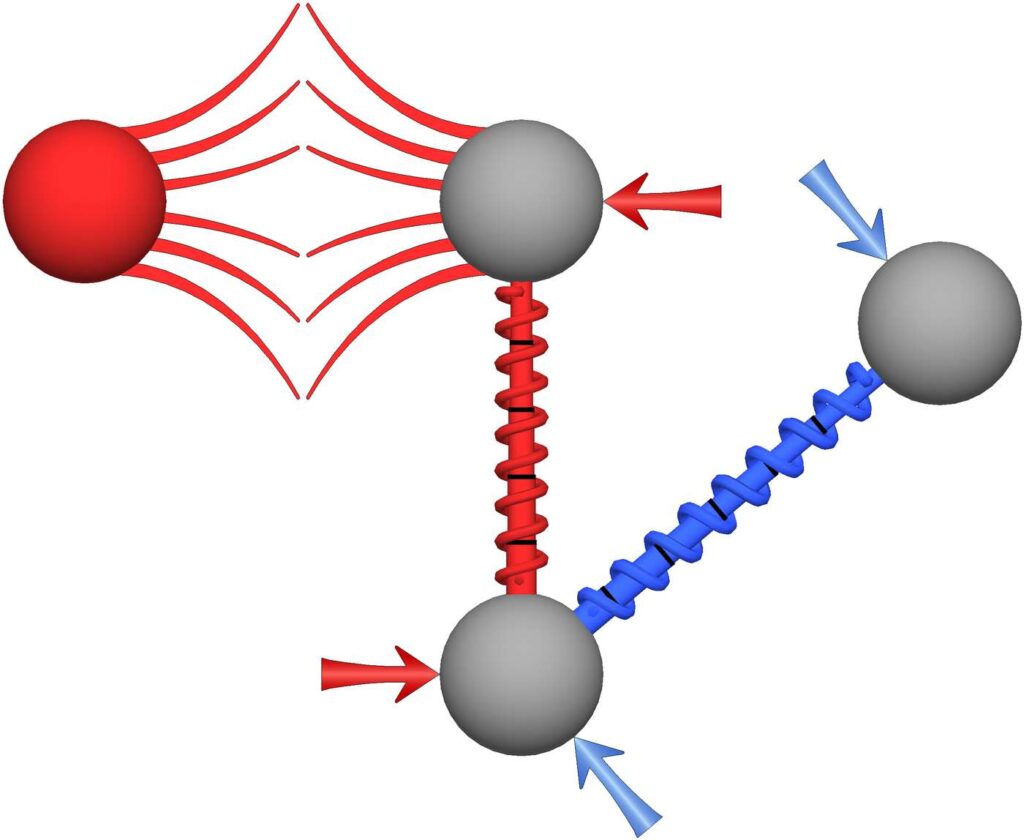
Figure 33. We have replaced the atoms from Figure 32 with balls joined together by frictionless telescoping rods. The angle between the rods is fixed by the lower ball. The springs provide a restoring force whenever the bond lengths vary from their relaxed values. Both the telescoping rods and the springs approach the limit of having no mass. This idealized hardware now matches the planar angle lock shown in Figure 32.
From physics, we know that physical hardware must always comply with the conservation laws. Moreover, the angle lock imposed by the physical hardware and the planar angle lock imposed at the atomic scale will both require the same combination of forces to keep their angles fixed for analogous collisions. So if the hardware forces needed to keep the angle fixed comply with the conservation laws at our scale, then the analogous forces at the atomic scale must also comply with the conservation laws.
We now accept that planar angle locks are fully compliant with the conservation laws as long as the locked planar angle is held exactly constant. Thus, we also confirm that planar angle geometry locks are acceptable in this free will paradigm.
Lastly, let us briefly cover what is happening in Figure 32 and Figure 33. In this collision, in order to keep the angle locked, the sum of the forces shown will accelerate the body of the three atoms rightward and put this body into a clockwise rotation. Simultaneously, the incoming particle will lose energy. The end result is that energy, momentum, and angular momentum will all be conserved.
The Dihedral Angle Geometry Lock
Again, a dihedral angle is a three-dimensional angle formed by three bonds, as shown below in Figure 34. For a mind to impose a geometry lock on a dihedral angle, the mind will have to have governing control over the three bonds that form the dihedral angle.
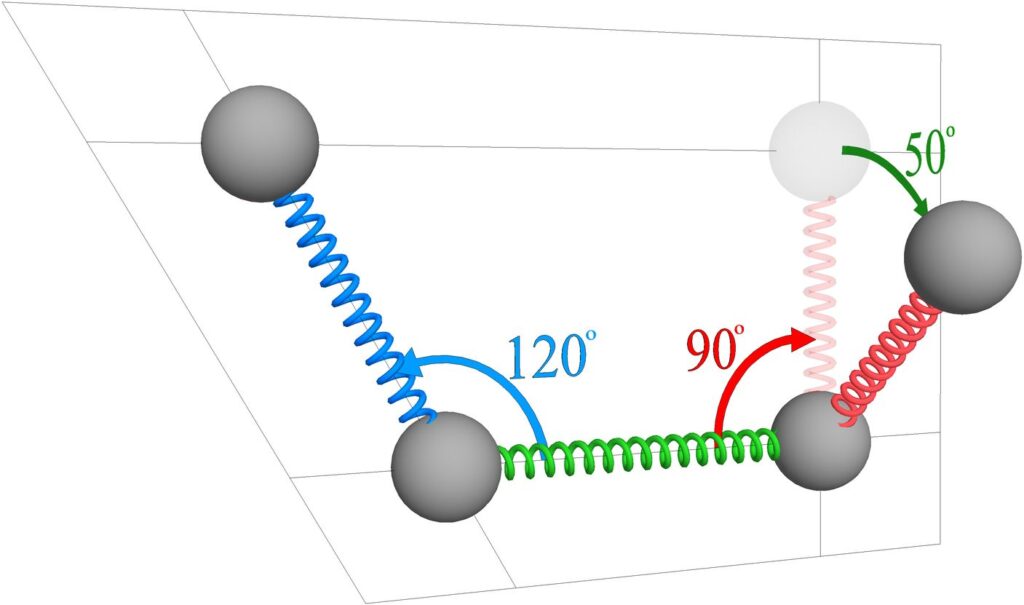
Figure 34. A dihedral angle is formed by three bonds. These three bonds also form two planar angles.
Notice that a dihedral angle includes two planar angles. In the figure above, the blue and green bonds form a planar angle of 120°, while the green and red bonds form a planar angle of 90°. The dihedral angle in the figure is 50°.
We will now show the forces needed to lock the dihedral angle above when it is being acted upon by an external force.
Dihedral Angle Locking Forces
The mind forces shown in Figure 35 are holding a dihedral angle lock during a collision with an incoming particle. In this example, the planar angles and the bond lengths are not locked, the mind is only holding a lock on the dihedral angle. Recall that the colors of the force arrows correspond to the colors of the bonds that the forces are acting across. The equal and opposite torques created by the blue and red torque pairs are responsible for locking the dihedral angle.
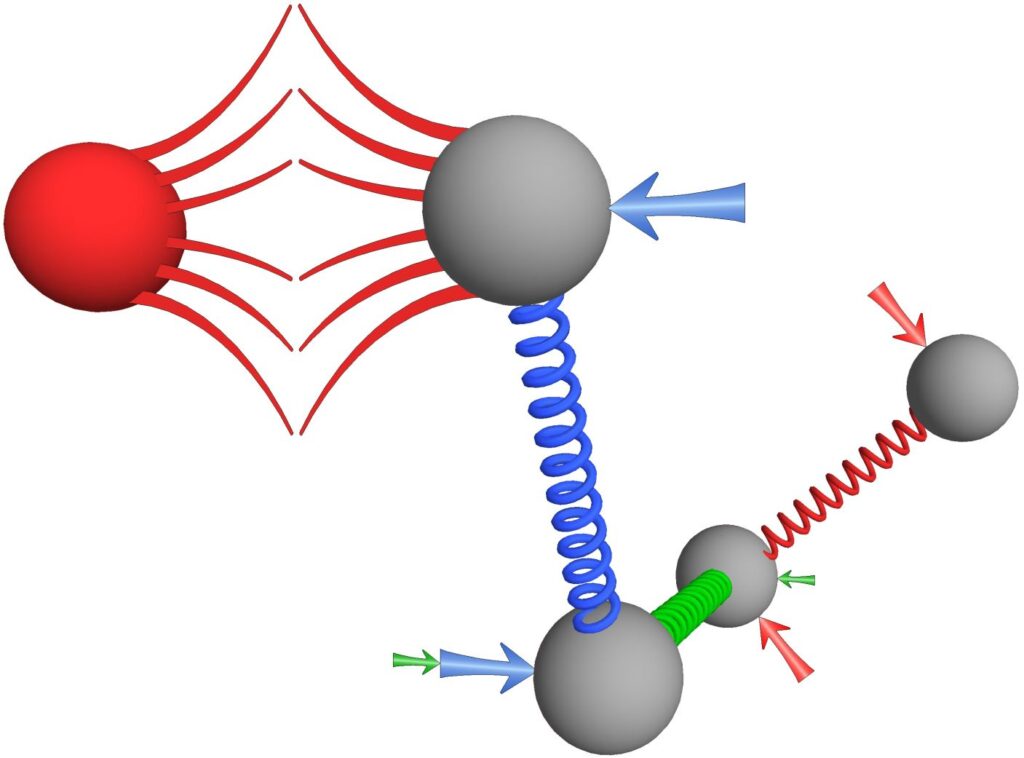
Figure 35. The geometry of the three bonds shown here is the same as that shown in the previous figure. A mind is holding its dihedral angle lock even as the structure endures a collision from the red particle approaching from the left. The collision force shown here is acting directly against the dihedral angle. The arrows indicate all the instantaneous, zero-sum mind forces needed to hold the dihedral angle constant at this single moment in time.
For the more physics advanced readers, there is an additional torque component that we have to address because of the 120° planar angle formed by the green and blue bonds. Because this planar angle is not 90°, the blue mind force pair is creating an additional torque component about the vertical axis that needs to be zeroed out. The green forces shown are acting across the green bond, and this green torque pair zeroes out the extra vertical torque component created by the blue forces.
The sum of all the mind forces and torques shown in Figure 35 is zero, so the mind is complying with the zero-sum rule. Again, these mind forces and torques are doing both positive work and negative work during this collision, but once again, the sum of the work done will necessarily be zero as long as the dihedral angle is held constant.
As with all geometry locks, to comply with the conservation laws, dihedral angle locks can only be imposed at a moment when the dihedral angle is not changing. As always, any geometry lock can be released at any time because the act of releasing a geometry lock does not affect the energy, momentum, or angular momentum of a system.
Geometry Locks in Combination
The three types of geometry locks are orthogonal to one another. This means that the mindshell can impose any geometry lock without considering what it is doing with any other geometry lock.
Furthermore, there is no overlapping of geometry locks nor is there any geometry beyond the reach of geometry locks. For this reason, the three types of geometry locks together form a complete orthogonal set. As a result, when a mind locks all the bond lengths, all the planar angles, and all the dihedral angles of a material body at the same time, the mind is creating a rigid body with a temperature of absolute zero. A material body that has been made fully rigid by geometry locks will necessarily have no relative motion because any motion within a fully locked body would violate energy conservation.
Minds Exert Forces on Nucleons
Geometry locking becomes problematic when we attempt to understand exactly how the mindshell exerts forces on the atoms involved. This is because atoms are made up of many component particles that are all in relative motion. Does the mindshell exert many independent forces simultaneously on all the wavelike component particles of each atom?
It turns out that so complex a solution is not necessary. To impose a length lock on a bond, the mindshell needs to exert a force on only one particle in the nucleus of each atom. That is, length locks will be imposed by locking the distance between two nucleons, one nucleon from each atom. To comply with the conservation laws, length locks must be imposed when there is no relative motion between these two nucleons, and the lock must keep the distance between these two nucleons constant. Length locks, therefore, do not lock the distance between the centers of mass of the two atoms, only the distance between the two nucleons that are being locked.
Similarly, when a mindshell imposes a planar angle geometry lock, the mindshell will act on three nucleons, one nucleon from each of the atoms forming the planar angle, and the same principle will apply to dihedral angle geometry locks.
Protons and neutrons are themselves made up of quarks, but we are working with principles here, so we will restrict our discussion to the more familiar level of nucleons.
The Time Scale of Consciousness
Because consciousness is massless and momentum free, consciousness has no physical scale – it is neither big nor small. We now turn our attention to the time scale of consciousness. We found that consciousness imposes geometry locks at the moment the geometry to be locked has become motionless. For specificity, we will consider the length lock.
The mindshell imposes a length lock at the moment the distance between the two nucleons to be locked becomes constant. This is the moment the kinetic energy between the nucleons is exactly zero. If the mind were to impose the length lock before or after this moment, the mind forces would be violating the conservation laws. But how could a mind impose a geometry lock exactly at this infinitesimally small unit of time?
It turns out that the time a bond spends at the zero kinetic energy level is not infinitesimally small. In quantum physics, the energy of a bound system is restricted to discrete values, so a vibrating bond will spend a discrete amount of time at the zero kinetic energy point. While it is true that the unit of time we are discussing here is unfathomably small, it is non-zero, and non-zero is all we need to make this time span acceptably large for the computer-like, deterministic mindshell.
We have accepted that free will is real, and to be real, minds must be able to exert forces that change physical outcomes without violating the conservation laws. To do this, the mindshell must be able to impose geometry locks at moments in time corresponding to individual quantum energy level changes. Therefore, this free will paradigm accepts that the mindshell operates on a time scale commensurate with changes in discrete quanta of energy.
Nucleons Bound to a Bound System
For specificity, we will again focus on length locks.
In the last section, we found that it would be impossible to impose geometry locks at infinitesimally small units of time. However, the atoms of molecules belong to a bound system, and bound systems are restricted to discrete energy levels. This gave us finite units of time for imposing geometry locks, thus making geometry locks possible.
However, it is the two atoms that belong to the bound system of a molecule, not the two nucleons that are actually being locked. If the two nucleons that are actually being locked are not bound to one another, then would their relative kinetic energies still be restricted to discrete values? If not, then we would be back to minds applying length locks at infinitesimally small units of time and the solution above would fail.
While the two nucleons are not bound directly to one another, the two nucleons are bound to the nuclei of the two atoms that are in turn bound to one another. This means the energy of these nucleons will be restricted to discrete values relative to their atoms, and the energy of the atoms will be restricted to discrete values relative to one another. Thus, the energy of the nucleons relative to one another will also be restricted to discrete values.
The Mind Force Is a Fundamental Force
Minds cannot impose forces by generating an electric field or any other type of field, for the remnants of these fields would also accelerate the surrounding charged particles that are not being locked, and this would violate the conservation laws. Therefore, a mind force must act directly on each elementary particle that is involved in a geometry lock. This requires the mind force to be a fundamental force.
Making Collision Forces Predictable
The mind forces needed to hold geometry locks must exactly match the external collision forces acting on the atoms. However, the external collision forces acting on a locked geometry are continuously changing in a seemingly unpredictable way, so how does the mindshell know what force it will need to apply in the momentary future so that its own mind forces will exactly match the upcoming collision forces.
This is the reason the mindshell must exert geometry locking forces within the nuclei of the atoms it is locking. The nucleus is surrounded by an electron cloud that will be responding continuously to the external collision forces. The mindshell will read the ongoing response of the electron cloud to the external collision forces, and it will deterministically use the information from the distant electron cloud to continuously create the counterforces needed to hold its lock on the nucleon pairs.
It is the distance between the nucleons and the electron cloud that gives the mindshell the predictive information it needs to deterministically compute the counterforces that will be needed in the momentary future to maintain geometry locks during collisions. Once again, we find that a mind is able to sense the electron cloud of the atoms it governs.
Length Locks for Shared Bonds
Recall that adjacent minderelles share governing control over their common bond. If these two minds were to impose a length lock on the same nucleons at the same time, each minderelle would be exerting the forces needed to exactly counter the external forces acting on the nucleons. This doubling up of mind forces would create a total mind force equal to twice the external force, and this would cause the two nucleons to accelerate which would lead to a violation of the conservation laws. So how can two minderelles share governing control over the same molecular bond without any risk of violating the conservation laws?
There are multiple ways this can be done. To make this free will paradigm acceptable, we need only present one to show it is possible.
We begin at the moment the shared bond is first formed between the two minderelles. Upon the formation of this shared bond, there will be a communication handshake between the two mindshells, similar to what happens when computer network connections are first made. The mindshell on the nitrogen side will assume governing control over one nucleon from each side of the shared bond, and it will impose a length lock on these two nucleons. This length lock will identify to the carbon side mindshell the two nucleons governed by the nitrogen side mindshell.
The mindshell from the carbon side of the bond will respond by assuming governing control over a different pair of nucleons and imposing a length lock on these two nucleons. This will identify the nucleons governed by the mindshell on the carbon side of the shared bond. From this point forward, one mindshell will only be able to initiate a length lock on its own nucleon pair if the other nucleon pair is currently in motion. (We cannot have both nucleon pairs locked simultaneously because we would lack the predictive information needed to hold the geometry locks.)
The Affective States of Consciousness
The affective states of consciousness span from euphoria, love, courage, and excitement to depression, hatred, anger, and fear, and for our purposes will also include hallucinations, confusion, drunkenness, possibly pain, and so on. These affective states dramatically impact how we experience life. Affective states are such an intrinsic part of the conscious experience that there can be no conscious experience free of any affective state.
We also know that affective states do not always come from within the consciousness of the minderelle itself; we can take drugs that will alter our affective state – alcohol, opioids, LSD, marijuana, caffeine, and so on. But when a human takes an opioid, how does the human brain change the inputs to the primary in such a way that the person feels euphoria?
There are several possibilities based on the material covered in Chapter 12. It is possible the minderelle was divine designed so that the mindshell timer cycle includes a time slot dedicated to the affective state of consciousness. Or the affective state of the primary could be influenced by the data that entering through the hydrogen bond of the primary. But there is another possibility we have not discussed.
Perception of Photons and Sound
Minderelles working together have created complex biological systems. Our eyes capture images of our surroundings by focusing and then detecting photons. Our ears capture the sounds of our surroundings by detecting and processing sound waves. Our vision and hearing are both highly complex systems that not only include the eyes and ears themselves, but also the highly complex areas within the brain where this visual and sound data is analyzed and processed.
The highly complex visual and audio processing parts of the brain had to be engineered by the mindcores of minderelles because the mindshell can only perform fully determined functions and engineering is not a determined function. But before the mindcores could begin engineering visual and audio systems, these mindcores first had to know that photons and sound waves existed. This leads us to conclude that the mindcore must in some way experience both the photons and the sound waves coming in from their surrounding environment.
The question is, when a photon or sound wave transfers momentum to a minderelle, how is the mindcore informed of this event? A single photon striking an amino acid is not the delivery of a complete, or even a partial, image. Moreover, one impinging photon does not deliver information that is properly formatted for the visual sensory field, nor for any other sensory field for that matter. As well, photons and sound waves will arrive at random times in the minderelle’s timer cycle, so these arrival times will not be synchronized with any specific sensory field time slot. For these reasons, it seems that the mindcore could not be informed of impinging photons and sound waves through the sensory fields.
This raises the possibility that photons and/or sound waves could alter the mindcore’s affective state of consciousness. If photons alter a minderelle’s affective state of consciousness, then brains could have evolved to biologically generate photons and/or sound waves directed towards the primary, as well as other minderelles of the brain, for the specific purpose of altering the affective state of consciousness. This could be done to provide incentives, disincentives, to accompany informational content, and so on.
In any case, because drugs cause changes in the affective state of consciousness, we know the brain is capable of interacting with the primary in a way that brings about these affective state changes. Whatever the mechanism used by the brain to alter the affective state of consciousness, all mindshells will bring on the same affective state of consciousness with the same affective state input because all like entities must function alike.
However, while mindshells are all identical entities, brains are not. Each brain is unique, and this is even true within the same species. Therefore, there may also be variations in the affective state inputs to the primary for any given drug.
Photon Capture and Release
Photon energy can sometimes be absorbed by molecules. The absorbed photon energy may raise the energy level of an electron, it may increase the vibrational energy of the molecular bonds, or it may raise the nuclear energy level, depending on the energy of the incoming photon. We already know that minds can lock in the energy held within the molecular bonds using geometry locks, so minds will be able to capture the energy from photons by locking in higher energy states.
We have also found that minds can detect external forces acting on their electron clouds. However, if external forces acting on the electron cloud affect the thoughts of the mind, then by Newton’s third law, the mind should be able to exert forces on the electron cloud. This raises the possibility that minderelles may be able to lock and release the energy levels of their electrons.
We also found that minds impose geometry locks across molecular bonds by acting on the particles within the nucleus, so we now have minds acting on all the matter over which the mind has governing control. As with geometry locks, these energy level locks could be released at any time without violating any of the conservation laws.
This means it should be possible for minderelles to capture photon energy and then release that energy at the time of their choosing. If this is true, then we may be able to communicate with the primary of a protein through photon (or sound energy) exchange, keeping in mind that different frequencies of photons and sound may bring on different affective states of consciousness which may impact communication efforts.
Problematic Molecular Structures
In Chapter 3, we found that for the universe to be knowable, only a single molecular structure could host all conscious minds throughout the universe. So if there are any differences in the molecular electronic configuration of two molecules and one is alive, then the other cannot be alive.
However, chemical bonds are often described as single bonds or double bonds, descriptions that for our purposes may be oversimplified. Experts in molecular chemistry will have to determine if a more detailed mapping of the full electronic configuration of the mind signature is needed to ensure that we can always positively distinguish between living matter and natural matter.
There are two (hypothetical?) molecules that warrant special attention. These two molecules are shown in Figures 36 and 37.
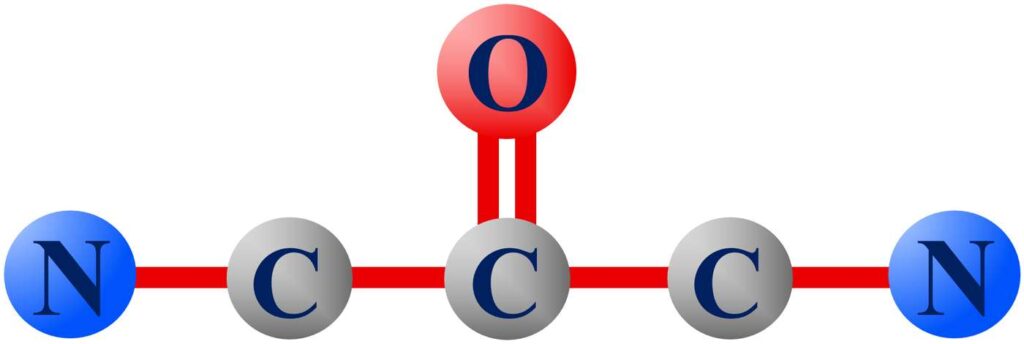
Figure 36. If this molecule exists or were created, would it support the life of a mind?
The second molecule of interest, shown below, centers on the nitrogen atom.
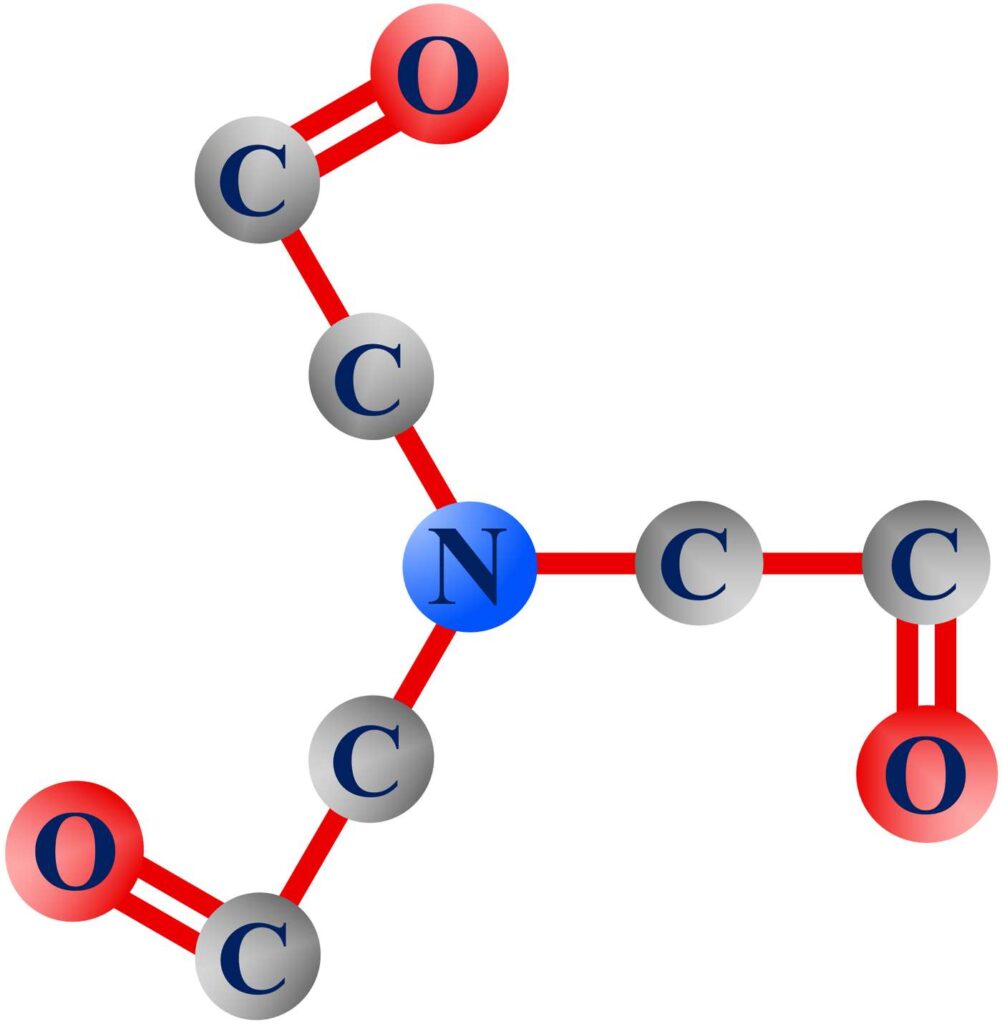
Figure 37. The electronic configuration of this molecule would also need to be fully mapped to understand if there are asymmetries that would make consciousness possible, or if not, to determine how it is distinguishable from the mind signature.
If one of the molecules shown contains living matter, there would have to be an asymmetry within that would make it possible to identify which atoms support the presence of the mind. On the other hand, if these molecules do not support life, then the electronic configurations within would have to be distinguishable from the electronic configuration of the mind signature. There are other molecules of interest as well, such as guanine.
The author does not have sufficient expertise in the electronic configurations of molecular structures to work through these details.